算法——24点游戏
2019-06-17 Algorithm Java给定四个1-10的正整数,可以进行+ - * / 四种运算,每个数字只能用一次,任意组合构造表达式使结果为24,要找出所有可能的组合?
解题思考
初拿到题目最先想到的就是穷举法了,我们先假设四个数字为A、B、C、D,然后穷举所有的可能性,简单算一下可以得到一共有4! * 4^3 = 1536种可能性,如下图所示:
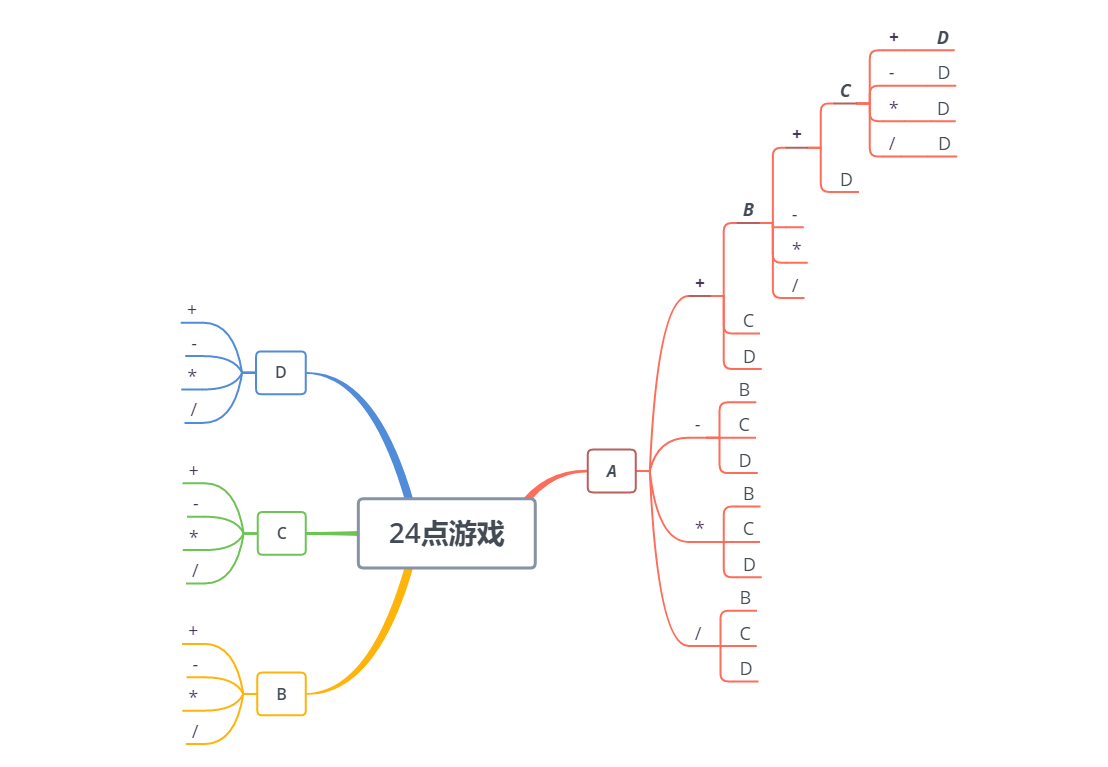
DFS解法
DFS是Depth-First search 深度优先搜索的简称,与其对应的还有BFS(Breadth-First-Search 广度优先搜索),在这里我们使用递归的方式深度优先遍历搜索树找到所有可能性,然后根据得出的算术表达式(如1+2+3*4)计算并判断筛选出计算结果为24的组合,代码如下:
import java.util.*;
import java.util.regex.Pattern;
import java.util.stream.Collectors;
/**
* @author JianhuiChen
* @description 24点游戏
* @date 2019/6/18
*/
public class Count24 {
public static void main(String[] args) {
List<String> results = permutation(Arrays.asList(1, 2, 3, 4),
Arrays.asList(Operator.PLUS, Operator.MINUS, Operator.MULTIPLY, Operator.DIVIDE));
results.stream()
.filter(express -> expectCalc(express, 24))
.forEach(System.out::println);
}
private static List<String> permutation(List<Integer> numbers, List<Operator> operators) {
return permutation(numbers, operators, null);
}
/**
* 深度优先搜索策略得出所有的组合可能性
*
* @param numbers 参与选择的数字
* @param operators 参与运算的运算符
* @param expressRecord 算术表达式记录值
* @return 可能性组合
*/
private static List<String> permutation(List<Integer> numbers, List<Operator> operators, String expressRecord) {
if (expressRecord == null) {
expressRecord = "";
}
List<String> resultList = new ArrayList<>();
for (int num : numbers) {
if (numbers.size() == 1) {
// 只剩一个数字未选时退出循环
resultList.add(expressRecord + num);
break;
}
for (Operator oper : operators) {
// 过滤掉已选项
List<Integer> optional = numbers.stream()
.filter(n -> n != num)
.collect(Collectors.toList());
resultList.addAll(permutation(optional, operators, expressRecord + num + oper));
}
}
return resultList;
}
/**
* 进行预期运算
*
* @param aritExpression 算术表达式
* @param targetVal 目标值
* @return 是否符合预期
*/
private static boolean expectCalc(String aritExpression, int targetVal) {
return calculation(aritExpression) == targetVal;
}
/**
* 根据算术表达式求值
*
* @param aritExpression 算术表达式 exp: 4*2/1*3
* @return 计算结果
*/
private static int calculation(String aritExpression) {
// 将表达式根据运算符切割
StringTokenizer tokenizer = new StringTokenizer(aritExpression, "+-*/", true);
Stack<Double> numStack = new Stack<>(); // 存放数字
Stack<Operator> operStack = new Stack<>(); // 存放操作符
String currentEle; // 当前元素
while (tokenizer.hasMoreTokens()) {
currentEle = tokenizer.nextToken().trim(); // 去掉前后的空格
if (!"".equals(currentEle)) { // 只处理非空字符
if (Pattern.matches("^\\d+(\\.\\d+)?$", currentEle)) { // 为数字时则加入到数字栈中
numStack.push(Double.valueOf(currentEle));
} else {
Operator currentOper = Operator.getOperatorBySymbol(currentEle);//获取当前运算操作符
if (currentOper == null) {
throw new RuntimeException("存在无效的操作符" + currentEle);
}
while (!operStack.empty() && operStack.peek().priority() >= currentOper.priority()) {
compute(numStack, operStack);
}
// 计算完后把当前操作符加入到操作栈中
operStack.push(currentOper);
}
}
}
// 经过上面代码的遍历后最后的应该是nums里面剩两个数或三个数,operators里面剩一个或两个运算操作符
while (!operStack.empty()) {
compute(numStack, operStack);
}
return numStack.pop().intValue();
}
/**
* 取numStack的最顶上两个数字
* operStack的最顶上一个运算符进行运算
* 然后把运算结果再放到numStack的最顶端
*
* @param numStack 数字栈
* @param operStack 操作栈
*/
private static void compute(Stack<Double> numStack, Stack<Operator> operStack) {
Double num2 = numStack.pop(); // 弹出数字栈最顶上的数字作为运算的第二个数字
Double num1 = numStack.pop(); // 弹出数字栈最顶上的数字作为运算的第一个数字
Double computeResult = operStack.pop().compute(num1, num2); // 弹出操作栈最顶上的运算符进行计算
numStack.push(computeResult); // 把计算结果重新放到队列的末端
}
/**
* 支持的运算符
*/
private enum Operator {
PLUS("+") {
@Override
public int priority() {
return 1;
}
@Override
public double compute(double a, double b) {
return a + b;
}
},
MINUS("-") {
@Override
public int priority() {
return 1;
}
@Override
public double compute(double a, double b) {
return a - b;
}
},
MULTIPLY("*") {
@Override
public int priority() {
return 2;
}
@Override
public double compute(double a, double b) {
return a * b;
}
},
DIVIDE("/") {
@Override
public int priority() {
return 2;
}
@Override
public double compute(double a, double b) {
return a / b;
}
};
Operator(String symbol) {
this.symbol = symbol;
}
/**
* 运算符
*/
private String symbol;
/**
* @return 运算优先级
*/
public abstract int priority();
/**
* @param a 第一个运算数
* @param b 第二个运算数
* @return 两个数对应的运算结果
*/
public abstract double compute(double a, double b);
/**
* 根据运算符查找运算操作类
*
* @param symbol 运算符
* @return 运算操作类
*/
public static Operator getOperatorBySymbol(String symbol) {
for (Operator operator : Operator.values()) {
if (symbol.equals(operator.toString())) {
return operator;
}
}
return null;
}
@Override
public String toString() {
return symbol;
}
}
}
输入2、4、6、8能得到以下部分结果
2*6+4+8
2*6+8+4
2*6*8/4
2*6/4*8
2*8*6/4
2*8/4*6
2/4*6*8
2/4*8*6
2/8+4*6
2/8+6*4
4+2*6+8
4+6*2+8
4+8+2*6
4+8+6*2
4*6+2/8
4*8-2-6
...
优化思路
上述算法做了很多的重复计算,众所周知,加法和乘法是满足交换律的,所以如1*2*3*4这类组合任意排列所得的计算结果都是相同的,针对这部分我们可以如爬楼梯问题的备忘录算法缓存计算结果,防止重复计算。
题目拓展,添加优先级
我们简单的将上述的24点游戏扩展一下,除了数字和运算符我们再加上括号的选择,这个时候有多少种情况?代码该如何变更?其实简单想想加上括号即让任意组合如ABCD又演变出了五种加括号的方式((AB)C)D、(A(BC))D、(AB)(CD)、A(((BC)D)、A(B(CD)),然后根据括号运算搜索出正确答案即可,有兴趣的同学可以修改上述代码完成该题。